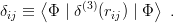
The probability of finding two constituents at the same position enters into the calculation of many properties of composite systems. This is the case for the hyperfine splittings in atoms, molecules, mesons or baryons, when one uses spin–spin forces of Breit–Fermi type, which have zero range. One may also mention some production rates or decay widths. In this section, we review some properties [100, 101, 98] of the matrix elements
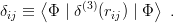 | (10.1) |
We already mentioned that, in the two–body case, the Schwinger rule (2.11), which can be
rewritten as 4πδ12 = μ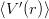 , is very useful for constraining δ
12 or for computing it in a reliable
way. Its generalization to the three-body case will lead to upper limits on δ12 for symmetric
baryons.
, is very useful for constraining δ
12 or for computing it in a reliable
way. Its generalization to the three-body case will lead to upper limits on δ12 for symmetric
baryons.