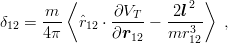
For non-central forces or bound states containing more than two constituents, Eq. (2.11) is rewritten as [100, 101]
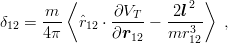 | (10.2) |
where V T is the total potential energy. For a symmetric baryon bound by pairwise, central forces, this is V T = V (r12) + V (r23) + V (r31). If one introduces the Jacobi variables (3.18) then
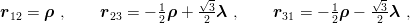 | (10.3) |
and the probability for quarks 1 and 2 to be on the top of each other is
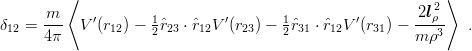 | (10.4) |
This expression was already written down by Cohen and Lipkin [102] in a different context. They neglected the small orbital term, and, using the virial theorem, arrived at interesting conclusions on the mass dependence of the correlation coefficients, to which we shall come back in Chapter 11. Here, we shall use Eq. (10.4) to derive rigorous bounds on δ12.