Properties of the wave functions

2.2 Properties of the wave functions

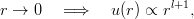
If V (r) is not too singular near the origin

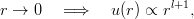r → 0 =⇒ u (r) ∝ rl+1,

(2.6)

For large r, u(r) decreases exponentially. If V (r) = Br^β, with β > 0, then

( ∘ ---- ) r → ∞ = ⇒ u(r) ∝ polynomial × exp − --2--- μBr1+ β∕2 . β + 2

(2.7)

The radial function of the (n + 1)^th state of given l, u_n,l(r), has n nodes r_i⁽ⁿ⁾, (i = 1,n) and according to the Sturm–Liouville theorem [22]

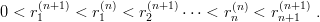0 < r(n+1 )< r(n)< r(n+1) ⋅⋅⋅ < r(n)< r(n+1) . 1 1 2 n n+1

(2.8)

The u_n,l satisfy the orthonormality condition

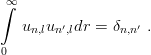∫∞ un,lun′,ldr = δn,n′ . 0

(2.9)

Note that the u’s can be chosen as real if V is real. For computing the leptonic width or the hyperfine splitting of S-states, one often needs the probability of finding the quark and the antiquark at the same place, i.e.,

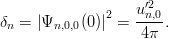′2 δ = |Ψ (0)|2 = un,0-. n n,0,0 4π

(2.10)

Thefollowing identity, attributed to Schwinger [17]

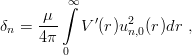∞ μ ∫ δn = --- V′(r)u2n,0(r)dr , 4π 0

(2.11)

turns out to be quite useful. While a rough variational or numerical solution often gives very bad estimates of Ψ_n,0,0(0), it becomes suprisingly accurate when δ_n is computed through the above integral.

[next] [prev] [prev-tail] [front] [up]