2.1 Basic equations

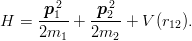
The simplest model of mesons describes them as quark–antiquark bound states of the nonrelativistic Hamiltonian

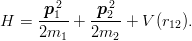(2.1)

V , the central part of the quark–antiquark potential, is flavour independent. It may be supplemented by spin–spin, spin–orbit, or tensor components to describe the fine or hyperfine structure of the multiplets, but we shall disregard these corrections here.

The centre-of-mass motion is removed by introducing the Jacobi variables

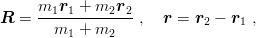(2.2)

as well as and 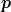, chosen as conjugates of 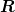and , respectively. Thus

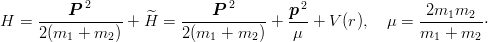(2.3)

Solving the eigenvalue equation 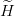Ψ = EΨ is most often achieved in spherical coordinates = (r,θ,φ). Owing the rotational invariance of the potential, bound states can be chosen with a well-defined angular momentum l. As explained in any standard textbook [21], introducing

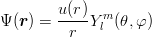(2.4)

leads to the radial equation

(2.5)

Note that we use ℏ = c = 1 very often in this review. States have the following indices: l for the angular momentum, m for the magnetic number (eigenvalue of l_z), and n for the number of nodes of u(r) in ]0, +∞[. Note that E and u(r) do not depend on m. The standard scheme for indices consists thus of: Ψ_n,l,m(), u_n,l(r), and E_n,l. Some indices are omitted whenever possible.