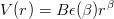
Power-law potentials exhibit simple scaling properties [17, 23]. If
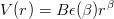 | (2.12) |
is an attractive potential (B is positive and ϵ is the sign function) and En,l(μ,B) the energy of a level of given n and l, then
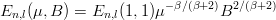 | (2.13) |
and the corresponding wave function scales as
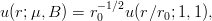 | (2.14) |
where the distance
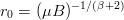 | (2.15) |
plays the role of a kind of
Bohr radius for the potential (2.12).
In a logarithmic potential, V = B ln r, the size of the wave function is governed by (2.14) with r0 = (μB)−1∕2, whereas the levels experience an overall shift when changing μ, since
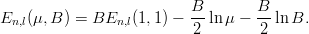 | (2.16) |
For fixed B, the levels spacings are independent of the reduced mass μ.
Scaling properties exist, in fact, for many potentials. For instance, to study the differents cases of the popular
Coulomb-plus-linear potential
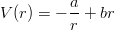 | (2.17) |
with various masses, it is sufficient to study the one-parameter family corresponding to a = μ = 1 and various values of b.