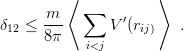
The result (10.5) can be generalized to any monotonically increasing potentials V such that V ′(r)∕r is decreasing, in the form
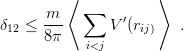 | (10.7) |
The proof is given in Ref. [98], in a polished form due to A. Martin. Some comments are in order:
i) The inequality is saturated in the harmonic-oscillator case. This explains why, with general potentials, the actual value is not too far from the bound, as seen previously in the linear case.
ii) For a power-law potential V = 1 2Brβ with 1 ≤ β ≤ 2, one can get a simple analytic bound on δ12 for the ground state by using the virial theorem and the variational principle. The sequence is
![( )
m 3βB ⟨ β ⟩(β−1)∕β m β 3B 1∕β (β−1)∕β
δ12 ≤ -------- r12 = ---- --- ⟨VT ⟩
8π 2( ) [ ]8π 2 ( ) [ ]
m β 3B 1∕β 2 (β−1)∕β m β 3B 1∕β 2 (β−1)∕β
= ---- --- ------E ≤ ---- --- ------Evar ,
8π 2 2 + β 8π 2 2 + β](baryon1430x.png) | (10.8) |
since the exact energy E is smaller than any variational approximation Evar. A trial wave function
of Gaussian shape Ψ( ,
, ) ∝ exp −1
2α(
) ∝ exp −1
2α(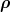 2 +
2 + 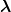 2) leads to
2) leads to
![[ β ]2∕(2+β)
3-2-+-β- β- Γ (32-+-2)-
Evar = m β 2mg Γ (3) ,
2](baryon1435x.png) | (10.9) |
so finally,
![( ) (β−1)∕β ( )1 ∕β [ 3 β ]2 (β−1)∕β(2+β)
-β- 3∕(2+β) 6- 3- β-Γ (2-+-2)
δ12 ≤ 8π (mg ) β 2 2 Γ (3) .
2](baryon1436x.png) | (10.10) |
iii) If the potential V grows faster than the harmonic oscillator, there are conflicting
contributions from the centrifugal barrier in Eq. (10.4) and from the terms in V ′ whose
expectation becomes larger than m∕8π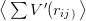 . There are cases where the latter effect
dominates. For instance, for V = 1
2Br3, the problem consists of comparing the zero-range
correlation with the mean separation. From an accurate hyperspherical calculation, one gets for
m = B = 1
. There are cases where the latter effect
dominates. For instance, for V = 1
2Br3, the problem consists of comparing the zero-range
correlation with the mean separation. From an accurate hyperspherical calculation, one gets for
m = B = 1
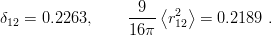 | (10.11) |
Hence the inequality (10.7) is clearly violated.
iv) There are in fact good reasons to believe that the inequality (10.7) is inverted if d∕dr(V ′∕r) > 0 everywhere. For perturbations around the harmonic oscillator, i.e., for V = r2 + λw(r), one already has
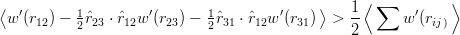 | (10.12) |
at first order, whereas the expectation value of 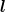 2
ρ contributes only at second order. A numerical
investigation shows that for V = r2.1 or even V = r2.01, one gets, indeed, the inequality
8πδ12 > m
2
ρ contributes only at second order. A numerical
investigation shows that for V = r2.1 or even V = r2.01, one gets, indeed, the inequality
8πδ12 > m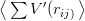 .
.