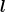 2
ρ and of
(
2
ρ and of
(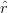 12 +
12 + 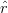 23 +
23 + 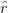 31)2, which ensures that
31)2, which ensures that 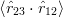 ≥−1
2, when the average is taken for a symmetric
wave function, one obtains
≥−1
2, when the average is taken for a symmetric
wave function, one obtains
Consider first a purely linear potential V (r) = 1
2br. From the positivity of 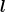 2
ρ and of
(
2
ρ and of
(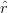 12 +
12 + 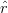 23 +
23 + 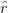 31)2, which ensures that
31)2, which ensures that 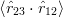 ≥−1
2, when the average is taken for a symmetric
wave function, one obtains
≥−1
2, when the average is taken for a symmetric
wave function, one obtains
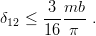 | (10.5) |
For m = b = 1, the bound δ12 ≤ 0.05968 is not too far from the exact values obtained in Chapter 5, which are
![+
[56,0 ] (n = 0) δ12 = 0.05689 ,
[56,0+ ]′ (n = 1) δ12 = 0.05664 .](baryon1425x.png) | (10.6) |
Note that δ12 depends slightly on n, unlike in the two-body case. The state with n = 1 contains
more contributions from higher hyperspherical harmonics, or, say, from configurations with internal
angular momenta lρ = lλ > 0 (still coupled by 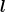 ρ +
ρ + 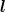 λ = 0), and this reduces the value of δ12. For a
collective linear potential V T ∝
λ = 0), and this reduces the value of δ12. For a
collective linear potential V T ∝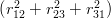 1∕2, which is exactly hyperscalar, the correlation
coefficient δ12 would be strictly independent of n.
1∕2, which is exactly hyperscalar, the correlation
coefficient δ12 would be strictly independent of n.