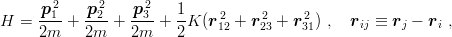
We start from the symmetric Hamiltonian
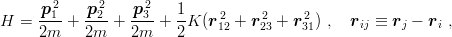 | (3.17) |
and introduce the Jacobi coordinates
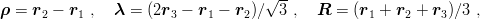 | (3.18) |
as well as their conjugate momenta 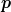 ρ,
ρ, 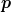 λ, and
λ, and 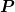 . This results in
. This results in
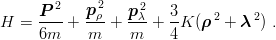 | (3.19) |
We now disregard the centre-of-mass kinetic energy which vanishes in the rest frame of the baryon. The Hamiltonian appears as the sum of two three-dimensional harmonic oscillators. We thus find the eigenvalues
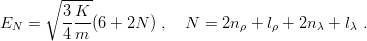 | (3.20) |
Using, again, the scaling laws of Section 2.3, which are immediately generalized to more than two bodies, one can assume that 3∕4K = m = 1.
The associated degeneracy is
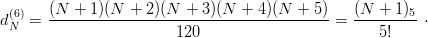 | (3.21) |
The index (6) reminds us that H can be viewed as a 6-dimensional oscillator. One can easily check the generalization dN(q+1) = (N + 1) q∕q! A basis for the eigenspaces is provided by states of the type
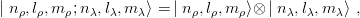 | (3.22) |
which can be arranged by Clebsch–Gordan coupling into states of given total angular momentum
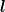 =
= 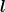 ρ +
ρ + 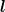 λ with the notations
λ with the notations
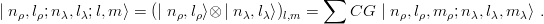 | (3.23) |
For N > 1, these states, however, do not exhibit simple permutation properties. To impose the restrictions of the Pauli principle, one should recombine the states (3.23) having the same N, l, and m into states of well-defined permutation symmetry. This will be done shortly, after some basic reminders about the permutation group S3.