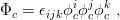
In quantum chromodynamics, the colour group is SU(3)c, where the indice is written to avoid confusion with the SU(3) group of flavour. In a baryon, the colour coupling of the three quarks to form a singlet, schematically
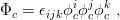 | (3.39) |
is antisymmetric under the exchange of the three quarks. This property is, in fact, one of the reasons for inventing colour [41].
Out of the spins of the two first quarks, one can build spin S = 0 and S = 1 states, which are respectively odd and even under P12, the exchange of these quarks. When supplemented by the third spin, they lead to one spin S = 3∕2 multiplet, which is symmetric, and two spin S = 1∕2 doublets, which are partners of mixed symmetry. These spin wave functions are
![| 3∕2, 3∕2⟩ = | ↑ ↑↑⟩
1
| 3∕2, 1∕2⟩ = √-[| ↓↑↑ ⟩+ | ↑↓↑ ⟩+ | ↑↑↓ ⟩]
3
-1--
| 3 ∕2,− 1∕2⟩ = √3-[| ↑↓↓ ⟩+ | ↓↑↓ ⟩+ | ↓↓↑ ⟩]
| 3 ∕2,− 3∕2⟩ = | ↓ ↓↓⟩](baryon1105x.png) | (3.40) |
and
![1
| 1∕2+λ ⟩ = √-[2 | ↑↑↓⟩− | ↓↑↑⟩− | ↑↓↑⟩]
6
+ -1--
| 1∕2ρ ⟩ = √2-[| ↑↓↑⟩− | ↓↑↓⟩]](baryon1106x.png) | (3.41) |
![− -1--
| 1∕2λ ⟩ = √6-[− 2 | ↓↓↑⟩+ | ↓↑↓⟩+ | ↑ ↓↓⟩]
1
| 1∕2−ρ ⟩ = √-[| ↑↓↓⟩− | ↓↑↓⟩].
2](baryon1107x.png) | (3.42) |
The formal analogy between the ∣1∕2λ⟩, ∣1∕2ρ⟩ pairs, and the Jacobi coordinates 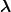 ,
, 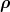 given in
(3.18) makes it clear that they have the same behaviour under permutations.
given in
(3.18) makes it clear that they have the same behaviour under permutations.
Isospin wave functions are built in exactly the same way, with ↑ replaced by u and ↓
replaced by d. States with three identical quarks such as those of the Ω− family (sss) have
a simple structure: either the spin wave function corresponds to spin S = 3
2 and the
space wave function has to be symmetric, or the total spin is S = 1
2 and one should
combine the corresponding spin wave functions with a pair of mixed-symmetry space
wave functions, as in Eq. (3.33), to form an overall spin–space wave function which is
symmetric. The above combinations are also found in qqq baryons made of ordinary
quarks (q = u or d), when isospin is I = 3∕2. This is the Δ family. When isospin is
I = 1∕2, i.e., for the nucleon family, new arrangements exist. First, isopsin I = 1∕2 and
spin S = 1∕2 can be combined to form a symmetric spin–isospin wave function. This is
what occurs for the nucleon itself and some of its excitations. The spin–isospin wave
function can also be of mixed symmetry and is associated with a mixed-symmetry spatial
wave function. Finally, there is the possibility of an antisymmetric spin–isospin wave
function which allows for the use of an antisymmetric spatial wave function such as
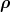 ×
×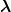 exp[−α(
exp[−α(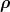 2 +
2 + 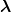 2)].
2)].