[next] [prev] [prev-tail] [tail] [up]

3.4 Permutation of three quarks

The 3! = 6 permutations of the quarks (1, 2, 3) are generated by the two operators

P→(1,2, 3) = (2, 3,1) , P12(1,2,3) = (2,1,3) .
(3.24)

There are three types of basic behaviour or, in other words, three types of irreducible representation of the group S3:

i) a symmetric behaviour (sometimes called

fully symmetric), for instance

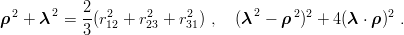2 2 2 2 2 2 2 2 2 2 ρ + λ = --(r12 + r23 + r31) , (λ − ρ ) + 4 (λ ⋅ ρ) . 3
(3.25)

ii) an antisymmetric behaviour (sometimes called

fully antisymmetric)

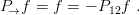P→f = f = − P12f .
(3.26)

Examples are

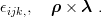ϵijk,, ρ × λ .
(3.27)

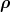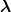iii) a behaviour of mixed symmetry, whose prototype are the Jacobi coordinates ρ and λ themselves. In Eq. (3.18), the third particle obviously plays a particular role, so let us redefine (we forget the vector character, which is not essential here)

(3) (3) ρ = ρ , λ = λ ,
(3.28)

and, similarly,

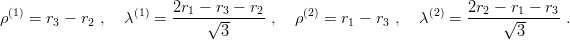2r − r − r 2r − r − r ρ(1) = r3 − r2 , λ(1) = --1--√-3----2 , ρ(2) = r1 − r3 , λ(2) = --2-√-1----3-. 3 3
(3.29)

Then, if the index i + 1 is computed modulo 3,

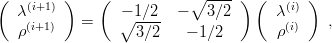( ) ( ∘ ----) ( ) λ(i+1) = −∘ 1∕2- − 3∕2 λ(i) , ρ(i+1) 3∕2 − 1 ∕2 ρ(i)
(3.30)

where, as expected, a rotation of angle 2π∕3 occurs.

A pair of mixed symmetry behaves like the real and the imaginary part of

z = λ + iρ ,
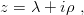(3.31)

on which the basic permutation operators act as follows:

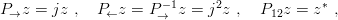P→z = jz , P←z = P→−1z = j2z , P12z = z∗ ,
(3.32)

where j = exp(2iπ∕3), as usual. The usefulness of this complex notation was often underlined [40]. It manifests itself when one analyses the permutation properties of a product of two irreducible representations. If one denotes the symmetric, antisymmetric, and mixed symmetry types of behaviour by S, A, and MS = MSλ + iMSρ, respectively, one easily gets the following rules

S ⊗ [S,A, MS ] = S, A,MS , A ⊗ [S, A,MS ] = [A, S,− iMS ] , MS ⊗ MS ′ = MS ′′∗ , MS ⊗ MS ′∗ = S + iA .
(3.33)

Any function of the three quarks can be separated into a sum of functions with basic behaviour, using the projector identities

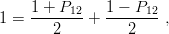1-+-P12- 1 −-P12- 1 = 2 + 2 ,
(3.34)

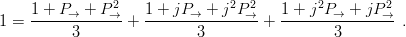1 + P→ + P2→ 1 + jP→ + j2P→2 1 + j2P→ + jP→2 1 = -------------+ ----------------+ ---------------- . 3 3 3
(3.35)

Consider, for instance, f = x1y3. Using (3.34) and (3.35), one gets

f = 1∕6 [ x1y3 + x2y3 + x2y1 + x3y1 + x3y2 + x1y2] +1 ∕6 [ x1y3 − x2y3 + x2y1 − x3y1 + x3y2 − x1y2] +1 ∕6 [2x y + 2x y − x y − x y − x y − x y ] 1 3 2 3 2 1 3 1 3 2 1 2 +1 ∕6 [2x1y3 − 2x2y3 − x2y1 + x3y1 − x3y2 + x1y2]
(3.36)

or, in short,

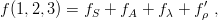f(1,2,3) = fS + fA + fλ + fρ′,
(3.37)

where the

prime emphasizes that the third and fourth terms are not partners of the same mixed symmetry doublet. There exists fρ and fλ′, which occur in other permutations of f. For instance,

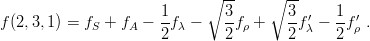∘ -- ∘ -- f (2, 3,1) = fS + fA − 1-fλ − 3fρ + 3f′λ − 1f ′ρ . 2 2 2 2
(3.38)

[next] [prev] [prev-tail] [front] [up]