The linear oscillator

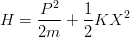
The one-dimensional harmonic oscillator is treated in any standard textbook [21]. The Hamiltonian

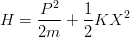P-2- 1- 2 H = 2m + 2 KX

(3.1)

is rewritten as

∘ --- ∘ ---[ 2 ] H = 1- K-h = 1- K-- − d---+ x2 2 m 2 m dx2

(3.2)

using the scaling transformation of Section 2.3 which reads here x = (Km)^1∕4X. The reduced Hamiltonian has eigenvalues

ϵ = 1 + 2n, n = 0, 1,2... n

(3.3)

and eigenfunctions

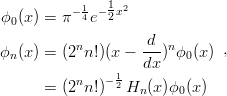ϕ (x) = π− 14 e− 12x2 0 n d--n , ϕn (x) = (2 n!)(x − dx) ϕ0 (x ) n − 12 = (2 n!) Hn (x )ϕ0 (x )

(3.4)

where H_n(x) is the Hermite polynomial

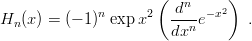( dn 2) Hn (x) = (− 1)nexp x2 --ne− x . dx

(3.5)