[prev] [prev-tail] [tail] [up]

3.7 Harmonic oscillator with unequal masses

For unequal masses, one may choose the Jacobi coordinates as

[ ]∘ ----------------------- m1r1 + m2r2 m3 (m1 + m2 )2 ρ = r2 − r1 , λ = r3 − ------------- ----------------------, m1 + m2 m1m2 (m1 + m2 + m3 )
(3.52)

so that a single reduced mass 2m1m2∕(m1 + m2) enters into the kinetic energy. We now restrict ourselves to the case of two different masses

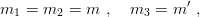m1 = m2 = m , m3 = m ′ ,
(3.53)

for which the harmonic oscillator is still exactly solvable. The Jacobi coordinates read

∘ --------- m ′ ρ = r2 − r1 , λ = [2r3 − (r1 + r2)] --------′ . 2m + m
(3.54)

The reduced part of the Hamiltonian

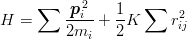∑ p 2 1 ∑ H = --i-+ -K r2ij 2mi 2
(3.55)

is

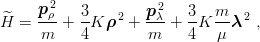2 2 ^ pρ- 3- 2 pλ- 3- m- 2 H = m + 4K ρ + m + 4K μ λ ,
(3.56)

with

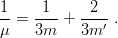1- -1-- -2-- μ = 3m + 3m ′ .
(3.57)

Factorization still works, so the energies are

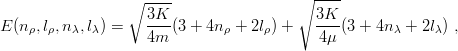∘ ---- ∘ ---- E (nρ,lρ,nλ,lλ) = 3K--(3 + 4n ρ + 2lρ) + 3K--(3 + 4nλ + 2lλ) , 4m 4μ
(3.58)

and the corresponding wave functions are

[ ] Ψ (n ρ,lρ,n λ,lλ;ρ, λ) = (α ρα λ)3∕4 Φnρ,lρ,m ρ(α ρρ)Φn λ,lλ,mλ(α λλ) , l,m
(3.59)

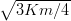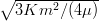where αρ = ∘ -------- 3Km ∕4 and αλ = ∘ -----2------ 3Km ∕(4μ). One should notice that if m′ > m, as in Λ, Λc, or Λb, then μ > m and the excitations of λ-type are lower than their analogues of ρ-type. The reverse is true if m′ < m.

[prev] [prev-tail] [front] [up]