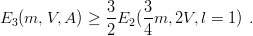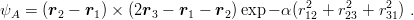[prev] [prev-tail] [tail] [up]

9.8 Generalization to excited states

Extending the inequalities to excited states, or to the sum of the first energies does not appear as an easy task. The

minimax principle [33] is not of immediate use here: for fixed r3, the wave function of a ground–state baryon, ϕ0(r1,r2,r3) and that of an excited state, ϕ1(r1,r2,r3) are not orthogonal with respect to integration over r1 and r2. For very special cases (harmonic oscillator, for instance) and for particular values of r3, ϕ0 and ϕ1 are not even linearly independent.

If one considers, however, our inequality (9.39) as relating the first symmetric level of the baryon spectrum and the first even level of the pseudomeson with quark mass 3m∕4, then a similar inequality holds between the first baryon with antisymmetric (A) spatial wave function and the first odd level of the pseudomeson

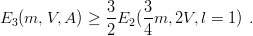E3 (m, V,A ) ≥ 3E2 (3m, 2V, l = 1) . 2 4
(9.62)

In the quark model this (A) state exists only for u and d quarks. A spin 1 2 wave function and an isospin 1 2 wave function, with mixed permutation symmetry, can be arranged in an antisymmetric spin–isospin wave function, which, in turn, can be combined to the colour wave function and this (A) spatial wave function in order to fulfil the Pauli principle. In the harmonic-oscillator model, this state with spatial wave function

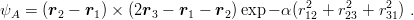ψ = (r − r ) × (2r − r − r )exp − α(r2 + r2 + r2 ) . A 2 1 3 1 2 12 23 31
(9.63)

is referred to by specialists as the [20, 1+], N = 2 state. With anharmonic confinement, this (A) state occurs at the top of the multiplet of positive parity excitations, as seen in Chapter 8.

[prev] [prev-tail] [front] [up]