[next] [prev] [prev-tail] [tail] [up]

9.7 The case of unequal constituent masses

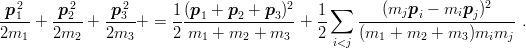
The extension of inequality (9.39) to baryons bearing different flavours is straightforward, but its practical consequences deserve some discussion. One easily rewrites the kinetic energy as

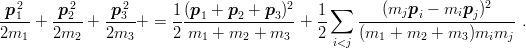p 2 p2 p 2 1 (p + p + p )2 1 ∑ (mjpi − mipj )2 --1-+ --2- + --3-+ = ----1----2----3-- + -- ----------------------. 2m1 2m2 2m3 2 m1 + m2 + m3 2 i<j (m1 + m2 + m3 )mimj
(9.54)

Thus if one introduces

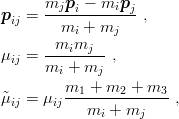p = mjpi--−-mipj- , ij mi + mj mimj μij = m--+--m--, i j μ˜ij = μijm1-+--m2-+-m3--, mi + mj
(9.55)

one can rewrite the reduced Hamiltonian of the baryon as

∑ [ p2 ] h3 = 1- -ij+ v (rij) 2 i<j ˜μij
(9.56)

leading to the lower limit

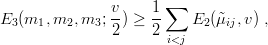v- 1-∑ E3 (m1,m2, m3; 2 ) ≥ 2 E2 (˜μij,v) , i<j
(9.57)

which usually corresponds to a very good approximation. There are, however, some new features:

– the limit is not saturated anymore in the harmonic-oscillator case, ∑ rij2 with equal strengths, but it is for strengths proportional to the product of the masses, ∑ mimjrij2 [86]

– the new limit (9.57) is not always better than the naïve limit (9.22).

Let us discuss this latter point in some detail, by considering two different masses, m1 = m2 = m, and m3 = M. We have to compare the two inequalities

[ ] v- 1- -2mM---- E3(m, m, M ; 2) > 2E2 (m, v) + E2 m + M ,v ,
(9.58)

v 1 m M [mM (M + 2m ) ] E3 (m, m, M ;-) > --E2( --+ --,v) + E2 ------------2--,v . 2 2 2 4 (M + m )
(9.59)

For M < 2m, the constituent masses in the new inequality (9.59) are always lighter than in (9.58), resulting in a better limit. For very large M, the above inequalities give respectively

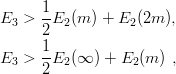1- E3 > 2 E2(m ) + E2(2m ), 1 E3 > --E2(∞ ) + E2 (m ) , 2
(9.60)

and the former is larger than the latter, because the ground-state energy E2 is a concave function of the inverse reduced mass, as seen in Chapter 2. For a power-law potential, rβ, the limits (9.58) and (9.59) are proportional to

A = 1-+ (--2x--)γ, 2 1 + x 1 1 x [x (2 + x)]γ B = -( -+ -)γ + --------2 , 2 2 4 (1 + x )
(9.61)

respectively, where γ = −β∕(β + 2) and x = M∕m. For x ≥ 8.4 in the Coulomb case β = −1, for x ≥ 12 in the case of a smooth r0.1 confinement, or for x ≥ 17.7 in the harmonic-oscillator case, one has A > B, so that the old limit is better than the new one. To illustrate the inequality (9.57), we choose in Table 9.3 several power–law potentials and the sets of constituent masses (m1,m2,m3) = (1, 1, 0.2) and (1, 1, 5) which are representative of the mass ratios involved in double-charm or single-charm baryons.

Table 9.3: Ground-state energy of qqQ compared with the lower limits of Eqs. (9.22) and (9.57) for some power-law potentials ϵ(β)rβ and quark mass ratios M∕m. The exact result corresponds to a hyperspherical expansion pushed up to a grand orbital momentum L = 8.

m = 1,M = 0.2
m = 1,M = 5
β 1 2 ∑ E2(μij)1 2 ∑ E2(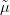˜μij) Exact 1 2 ∑ E2(μij)1 2 ∑ E2(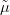˜μij) Exact
–1 –0.2083 –0.1451 –0.1398 –0.5417 –0.4618 –0.3848
0.1 1.9200 1.9432 1.9452 1.8239 1.8390 1.8486
1 4.5412 4.8982 4.9392 3.1411 3.3303 3.4379
2 6.6962 7.4498 7.5730 3.8238 4.1764 4.3729
3 8.3958 9.4978 9.7389 4.2712 4.7496 5.0166

[next] [prev] [prev-tail] [front] [up]