Mass dependence of the three-body binding energy

9.1 Mass dependence of the three-body binding energy

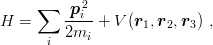
The Hamiltonian

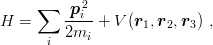∑ p2i H = ----+ V(r1, r2,r3) , i 2mi

(9.1)

depends linearly on the inverse of each constituent mass, so E₀(m₁,m₂,m₃), the lowest energy, is a concave function of each m_i⁻¹. This is an important consequence of the flavour independence of the central potential V .

As a first application [87], one may compare Λ_b(bud), Λ_c(cud), and Λ(sud) and get

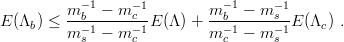m −1 − m −1 m −1− m − 1 E (Λb) ≤ --b−1-----c−1E (Λ ) + --b−1----s−-1E (Λc ) . m s − m c m c − m s

(9.2)

If the Hamiltonian is supplemented by spin–spin forces of the type

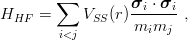∑ σi ⋅ σi HHF = VSS (r )-------, i<j mimj

(9.3)

where V _SS(r) is a flavour-independent short-range function, one keeps the linearity of the Hamiltonian in m₁⁻¹, and the inequality still holds. Another example is provided by the baryons with double flavour: Ξ_bb(bbq), Ξ_cc(ccq), and Ξ(ssq). If one uses the central Hamiltonian (9.1), one gets

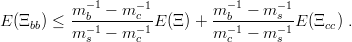m-−b1-−-m-−c1- m−b-1−-m-−s-1- E (Ξbb) ≤ m −1 − m −1 E(Ξ ) + m− 1− m − 1E (Ξcc) . s c c s

(9.4)

Hyperfine corrections (9.3) introduce terms in (m_Qm_q)⁻¹ still linear in m_Q⁻¹ and a term V _SS(r₁₂)m_Q⁻², which unfortunately has the wrong concavity in m_Q⁻¹, since V _SS(r) > 0 in most models.

To regain contact with the real world, consider the following sequence: Ξ^∗(ssq), Ω⁻(sss), and Ω_c^∗(ssc), all with spin 3/2. The Hamiltonian, including the hyperfine term, is linear in m₃⁻¹, so that

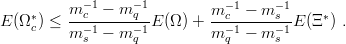m −1 − m −1 m −1− m −1 E (Ω∗c) ≤ --c−1-----q−1-E(Ω ) + --c−1-----s−1E (Ξ∗) . m s − m q m q − m s

(9.5)

The upper limits (9.2), (9.4) and (9.5) depend, however, on the quark masses, so that the comparison with experimental results is not immediate. It would be much more appealing to write down inequalities where the quark masses disappear and a direct comparison with experimental baryon masses is feasible. If one considers, for instance, the simple two-body result (2.43), Qq + qq < 2Qq , one is tempted to write down the following generalization to the three-body case

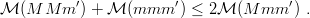M (M M m ′) + M (mmm ′) ≤ 2M (M mm ′) .

(9.6)

For m′ = m, this inequality is related to possible departures from the Gell-Mann–Okubo mass formula and, for m′ = M to the equal-spacing rule of the decuplet as we shall see in Chapter 11. Since the inequality (9.6) is satisfied in all numerical calculations based on reasonable potentials, it was believed for some time to be a general property of flavour-independent potentials. The situation was clarified by E. Lieb and further investigated by Martin et al.[88]. There are, in fact, counter-examples to (9.6), involving large mass ratios, for instance m′ = m ≫ M and very sharp potentials such as infinite square-wells. For smooth potentials suited for baryon spectroscopy, the inequality is satisfied in both m′ = m and m′ = M cases.

Similarly, one would very much like to compare the symmetric baryons Δ(qqq), Ω(sss) and Ω_ccc(ccc) to the recently identified Ξ_c(csq) baryon. The tempting inequality

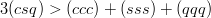3(csq) > (ccc) + (sss) + (qqq)

(9.7)

cannot be derived on the back of an envelope. Indeed, if one defines

-- 1 H = --[H (qqq) + H (sss) + H (ccc)] , 3

(9.8)

one immediately gets the result

-- 1- E0(H ) ≥ 3 [E0(qqq) + E0(sss) + E0 (ccc)] .

(9.9)

The trouble is that the true H(csq) contains not only the symmetric piece H but also a mixed symmetry piece, which lowers its energy. With realistic potentials, however, the inequality (9.7) is satisfied.

[next] [front] [up]