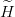 of Eq. (2.3) and denote by E(μ) one of the
eigenenergies and by ϕ(μ) the corresponding wave function. Obviously
of Eq. (2.3) and denote by E(μ) one of the
eigenenergies and by ϕ(μ) the corresponding wave function. Obviously
Let us once more consider the reduced Hamiltonian 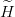 of Eq. (2.3) and denote by E(μ) one of the
eigenenergies and by ϕ(μ) the corresponding wave function. Obviously
of Eq. (2.3) and denote by E(μ) one of the
eigenenergies and by ϕ(μ) the corresponding wave function. Obviously
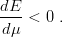 | (2.40) |
More precisely, from the Feynmann Hellmann theorem [33]
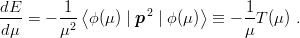 | (2.41) |
We also note that 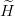 depends linearly on μ−1. We can thus use the general theorem that if a
Hamitonian depends linearly upon a parameter λ, its ground state energy is concave in
λ
depends linearly on μ−1. We can thus use the general theorem that if a
Hamitonian depends linearly upon a parameter λ, its ground state energy is concave in
λ
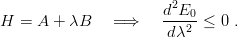 | (2.42) |
This follows from second-order perturbation theory or from the variational principle [33]. Here, once the constituent masses are added, one gets inequalities between the ground-state masses of any given angular momentum l
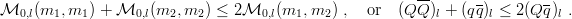 | (2.43) |
For instance, neglecting spin effects,
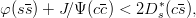 | (2.44) |
in agreement with experiment [5] (1.02 + 3.10 < 2 × 2.11 GeV). Similarly, one can derive
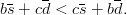 | (2.45) |
The convexity inequality (2.43) cannot be written for radial excitations: one should instead consider the sum of the n first levels.