9.3 Simple lower bound on baryon energies

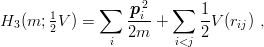
Let E₃(m; 1 2V ) be the lowest energy of a system of three identical quarks governed by the Hamiltonian

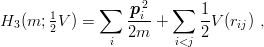(9.16)

where the 1/2 factor is introduced for convenience, even if one does not believe in the colour rule (9.10). Ader et al. [83] and, independently, Nussinov [84] have noticed that

(9.17)

In each bracket, the operator is bounded by its lowest eigenvalue E₂(m; V ) and hence

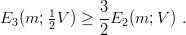(9.18)

In fact, this inequality is nothing but a slightly modified version of an old result derived in studies of self-interacting N-boson systems. The literature can be traced back from Refs. [85, 86]. One can, indeed, rewrite and generalize (9.18) as

(9.19)

so that, if V = −a∕r

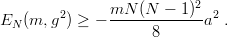(9.20)

Coming back to the hadron sector, we obtain for the ground states of mesons and baryons the amazingly simple inequality

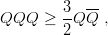(9.21)

meaning that a quark

weighs more in baryons than in mesons. A first generalization concerns unequal masses. One easily derives [84, 91]

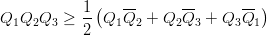(9.22)

provided that V _QiQj = 1 2V _{QiQ j} for each pair. Flavour independence is not necessary here.

Note, however, that some other generalizations do not hold. For instance, one may rewrite (9.18) as QQQ + Q Q Q ≥ 3QQ explaining why quark rearrangement is an allowed mechanism for a symmetric baryon–antibaryon annihilation. Now, if the mass ratio M∕m is large enough, one gets the inverted inequality

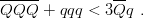(9.23)

An antibaryon with charm C = −3 would not annihilate on ordinary matter, and instead would scatter elastically until it decays weakly. In a flavour-independent potential, indeed, the heavy quarks preferentially remain together, to experience more binding. This effect is also responsible for the stability of the

tetraquark Q Q qq [83, 47].

Some spin effects can be incorporated in these inequalities [92]. Consider, for instance, a potential appropriate for S-waves

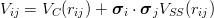(9.24)

with a central and a spin–spin piece, the latter being likely to depend on the quark masses, as per eq. (9.3). On can immediately compare spin 3∕2 baryons to vector mesons, by using the spin–triplet potential V _C + V _SS. Some examples follow (the experimental values [5] are shown for comparison, in units of GeV∕c²).

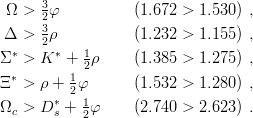(9.25)

We also have the predictions

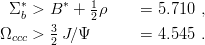(9.26)

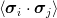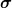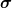In the spin 1 2 sector, one finds pairs with spin 1, i.e., σ_ij ≡ = 1, like ss in Ξ, pairs with spin 0, i.e., σ_ij = −3, like ud in Λ, and pairs in a mixture of spin 0 and spin 1 states. In a baryon such as Λ, σ_su = 0, whereas in a Σ, σ_su = −2. Since the Hamiltonian depends linearly on these _i ⋅_j, we can use the concavity theorem (2.42) to constrain the masses of fictitious mesons with σ = 0 or −2 from pseudoscalars and vectors

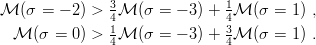(9.27)

Hence the inequality on qqQ states of Λ-type or Σ-type reads

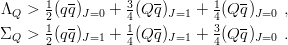(9.28)

Examples, are, in the Λ sector

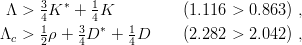(9.29)

and the prediction

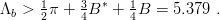(9.30)

In the Σ-sector

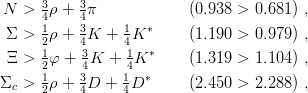(9.31)

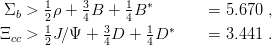(9.32)

For the Ξ_c and Ξ_c′, with quark content csu, one is tempted to write

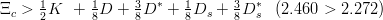(9.33)

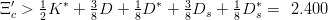(9.34)

In fact there is a mixing between the Λ-type and the Σ-type configurations. This pushes the Ξ′_c up, so that (9.34) is safe. It pushes the Ξ_c down but the effect is very small [93, 94], so that (9.33) is also guaranteed.