9.2 Relation between the quark–antiquark and the quark–quark potentials

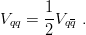
In simultaneous descriptions of the meson and baryon spectra, one often adopts the following relation between the quark–quark potential in a baryon and the quark–antiquark potential of quarkonia [89, 90]

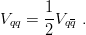(9.10)

This

1/2 rule works reasonably well phenomenologically. There are some arguments in favour of this rule, which are summarized below.

In the particular configurations where two quarks coincide, the third quark feels a localized colour 3 source, which behaves exactly as an antiquark and the above rule holds exactly. If one believes that the potential is pairwise, it can be expanded according to its colour structure in the t-channel: singlet exchange or octet exchange,

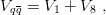(9.11)

and from simple SU(3)_c colour algebra

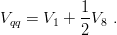(9.12)

The singlet-exchange piece cannot dominate or even contribute to confinement, otherwise all colour-singlet hadrons would be confined together. The simplest choice consists of assuming V ₁ = 0, leading to Eq. (9.10). Of course, one cannot eliminate the possibility of a non-confining piece of colour-singlet exchange.

Now, some three-body forces might well be present, making illusory the comparison of V _qq and V _qq . Fortunately, the situation is rather encouraging when one considers the most plausible model for interquark forces. The potential

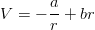(9.13)

is often interpreted as the superposition of one-gluon exchange, for which the

1/2 rule holds exactly, and a linear confinement corresponding to the shortest length of a chromoelectric flux-tube linking the quark to the antiquark. This is supported by lattice calculations, string models, flux-tube models, adiabatic bag models, etc. The most plausible generalization of br to baryons, with regard to gauge invariance, consists of the so-called

Y-shape potential [70] (already introduced in Chapter 7)

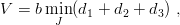(9.14)

It consists of the sum of the distances between the quarks and a

junction J, whose location should minimize the potential. One is back to a well-known

travelling salesman or

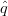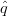road design problem, where the connection between given points should be accomplished at minimum cost. When the triangle q₁q₂q₃ has ordinary angles _i < 120^∘, the flux lines d _i make 120^∘ with respect to each other. If, say, ₁ > 120^∘, then the junction coincides with q ₁. One easily proves [70]

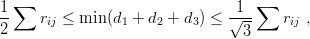(9.15)

so that the 1/2 rule is almost exactly satisfied and the departure goes in the right direction for the purpose of the inequalities we shall present in the rest of the chapter.