9.4 Improved lower bounds

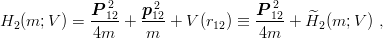
The inequality (9.18) provides a rather poor lower bound on the three-body binding energy. For instance, with m = 1 and V = r^0.1, one obtains E ₃ > 1.854 whereas the exact value is 1.880 ! To appreciate the crudeness of this lower limit, one may compare it to the upper limit E₃ < 1.883 which one obtains by a simple variational calculation using a Gaussian wave function. The reason for the discrepancy is simple. One starts from the decomposition (9.17) H₃ = 1 2 ∑ H₂(i,j) and replaces the energy of the two-body subsystem (i,j) by the ground state of H₂ at rest. However, the (ij) pair is actually not at rest in the baryon, and the corresponding kinetic energy is responsible for the sizeable departure of E₃ from its lower bound 3_ 2E₂.

The remedy consists of rewriting (9.17) in terms of reduced Hamiltonians whose eigenvalues are independent of the particular Galilean frame which is used. To this end, we define as in Eq. (2.3)

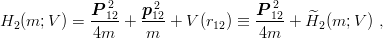(9.35)

and similarly

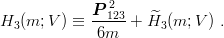(9.36)

Using the identity

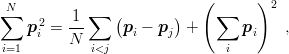(9.37)

we easily obtain

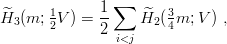(9.38)

from which one gets the improved lower limit on ground state

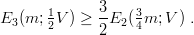(9.39)

The translation-invariant decomposition (9.38) was first written by Post [95] and was rediscovered independently in Refs. [85, 86]. The result (9.39) clearly constitutes an improvement with respect to the previous inequality (9.18) because the constituent mass in E₂ is decreased by a factor 3/4, and therefore the energy E₂ is algebraically increased. For an attractive power–law potential ϵ(β)r^β, this provides a factor (4∕3)^β∕β+2. A numerical comparison is shown in Table 9.1, where are listed the naïve lower limit (9.18), the improved lower limit (9.39), the exact energy obtained by hyperspherical expansion, and the variational bound derived from a Gaussian trial wave function. It is worth noticing that the new lower limit (9.39) becomes exact in the case of the harmonic oscillator. This is true for an arbitrary number N of bosons and the harmonic oscillator is the only potential for which the inequality is saturated. A beautiful proof of this property has been given by T.T. Wu and is written down in Ref. [86].

---

Table 9.1: Three-body ground state en ergy E₃(1; 1 2r^β) compared with the naïve lower limit 3_ 2E₂(1; r^β), the improved lower limit3 2E₂(3 4; r^β) and a simple variational limit approximation ₃ obtained with a Gaussian wave function

β	3 2E2(1)	3 2E2(3 4)	E3	3
–1	–0.37500	–0.28125	–0.26675	–0.23873
–0.5	–0.65759	–0.59746	–0.59173	–0.57964
0.1	1.85359	1.87916	1.88019	1.88278
0.5	2.75009	2.91296	2.91654	2.92590
1	3.50716	3.86013	3.86309	3.87114
2	4.5	5.19615	5.19615	5.19615
3	5.17584	6.15098	6.15591	6.17147

---

The inequality also becomes an equality to lowest order in perturbation for potentials

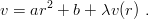(9.40)

As a consequence, the variational approximations E for E₃(m; 1 2V ) and E₂(3 4m; V ) with Gaussian trial wave functions satisfy the equality. For instance, for V = ϵ(β)r^β, one obtains

(9.41)