9.6 Connection to physical mesons

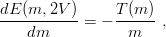
Here we keep the

1/2 rule of Eq. (9.10), connecting two-body potentials in baryons and mesons but we try to connect baryon masses to physical meson masses without using a specific potential. For simplicity we shall ignore spin effects. However, a pure spin–spin force could be included in our considerations, since it leaves the orbital momentum l as a good quantum number and does not introduce l dependence beside the centrifugal barrier in the radial equations.

The problem is that the new inequality (9.39) involves the unphysical quark mass 3m∕4 instead of the constituent mass m. However, we notice that, by the Feynman–Hellmann theorem [33]

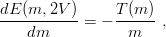(9.42)

where T is the expectation value of the kinetic energy in the ground state, and hence

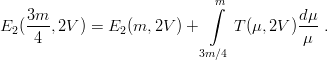(9.43)

There is an inequality on T(m) by Bertlmann and Martin [99]

(9.44)

where the energies appearing in the right-hand side are those of the ground state for angular momentum l = 1 and l = 0, respectively, in particular E₂(m) ≡ E₂(l = 0,m). Furthermore, if we impose the mild restriction that the potential satisfies

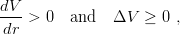(9.45)

which is an expression of asymptotic freedom (the colour charge seen increases with distance) and is valid for all existing models, phenomenological or QCD motivated, one can prove [99]:

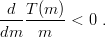(9.46)

Putting the above inequalities together results in

(9.47)

This inequality applies to binding energies as well as to hadron masses since one can add to both sides three times the quark constituent mass m.

For applications one cannot ignore spin completely. If the spin–spin potential is regularized, the derivation can be generalized for a spin-triplet state. To eliminate more or less the tensor and spin–orbit effects, one should average over the three spin-triplet P-states. Utilisation of (9.46) is more questionable. However, the range of integration in (9.43) is only a quarter of the mass, so that the uncertainty on T(m)∕m is not very large. We can try to apply this to the ρ − Δ comparison. If we follow the prescriptions of the Particle Data Group [5], the I^G = 1⁺ triplet P-states a_J are:

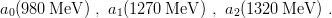(9.48)

This gives an average mass of 1265 MeV and leads, with m_ρ = 770 MeV, to

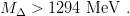(9.49)

We overshoot a little bit since M_Δ = 1238 MeV [5], but this was expected because of the crude treatment of spin effects, the neglect of the coupling to decay channels, etc. 

If we consider the centres of gravity of the hyperfine multiplets and incorporate the b(1233)(1⁺⁻) and the ρ − π (assuming that the hyperfine splittings are in the ratio 1 : −3), we obtain

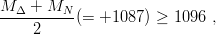(9.50)

in very close agreement. For the ϕ − Ω comparison, we need the ss  P-state average energy, and here we have only two candidates [5], f₁(1420 MeV) which is J^PC = 1⁺⁺ and f′ ₂(1525), J^PC = 2⁺⁺. Let us assume that they are not too far from the centre of gravity. Then we get, with M_ϕ = 1020 MeV,

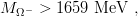(9.51)

in agreement with the experimental M_Ω⁻ = 1672 MeV [5].

We can also make predictions for the masses of the ccc and bbb baryons. With M_J∕Ψ = 3095 MeV and M_χc(triplet) = 3520 MeV, we obtain

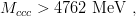(9.52)

and,with M_ϒ = 9460 MeV and M_χb(triplet) = 9900 MeV,

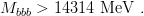(9.53)

The observability of the ccc baryon is considered to be possible by Bjorken [9], and would be very interesting [10].