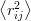 1∕2,
experiences the same value in the baryon as in the
1∕2,
experiences the same value in the baryon as in the
Within the above Gaussian approximation, the r.m.s. separation between quarks, dij ≡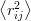 1∕2,
experiences the same value in the baryon as in the
1∕2,
experiences the same value in the baryon as in the
pseudomeson with constituent masses 3 4m. This approximation corresponds to choose the best harmonic approximation ar2 + b to the potential V . When one treats the anharmonicity λv(r) in perturbation, the pseudomesons, in comparison to baryons, receive large contributions from higher states of the harmonic oscillator. This results in larger shifts, hence in the inequality (9.39), and also in larger radii. An illustration is given in Table 9.2, where are compared the r.m.s. separation in baryons and pseudomesons, for (again !) simple potentials ϵ(β)rβ. Except for β = 2, the quarks are more tightly connected in baryons. The rigorous comparison of the dij’s is studied in a recent paper [96].
The situation is slightly more complicated when one compares the wave functions at a given
point. For instance, in Refs. [97, 98], the zero-range correlation in a baryon, δ12 = 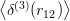 is
compared with its value in the pseudomeson. For a power–law confinement ϵ(β)rβ, δ
12 is
smaller than in the pseudomeson for β < 2, larger for β > 2 and equal for the harmonic
case β = 2. This result is rigorous for β ≤ 2, and in fact for any potential such that
d∕dr(V ′∕r) < 0 [98]. For β > 2, it is very plausible and has been checked by accurate numerical
calculations.
is
compared with its value in the pseudomeson. For a power–law confinement ϵ(β)rβ, δ
12 is
smaller than in the pseudomeson for β < 2, larger for β > 2 and equal for the harmonic
case β = 2. This result is rigorous for β ≤ 2, and in fact for any potential such that
d∕dr(V ′∕r) < 0 [98]. For β > 2, it is very plausible and has been checked by accurate numerical
calculations.
| β | d2 | d3 |
| –1 | 4.6188 | 4.5077 |
| –0.5 | 5.0905 | 5.0008 |
| 0.1 | 7.2883 | 7.2261 |
| 0.5 | 2.8182 | 2.8051 |
| 1 | 1.8794 | 1.8761 |
| 2 | 1.3161 | 1.3161 |
| 3 | 1.1069 | 1.1059 |