Ground-state baryons with central potentials

11.1 Ground-state baryons with central potentials

In the most elementary description of ground-state baryons, one would simply add the effective constituent masses, i.e., the masses would depend linearly upon the flavour numbers. Now, if one introduces a central, flavour–independent potential and solves accurately the three-body problem, one should hope to get something appreciably different. To measure to what extent this is true, let us define the scale-independent quantities

2[qqq ] + 2[qqs] − 4[ssq] R1 = -----------------------, [qqq ] − [sss]

(11.2)

2[sss ] + 2[ssq] − 4[qqs] R2 = -----------------------⋅ [qqq ] − [sss]

(11.3)

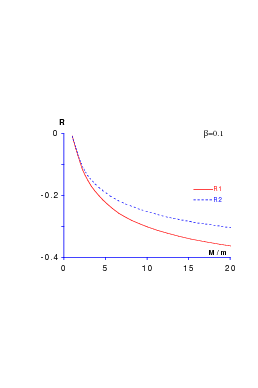
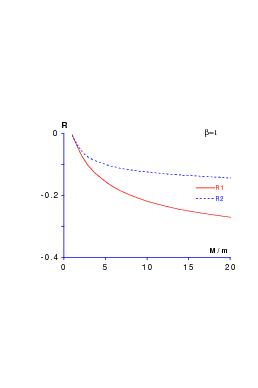
R₁ is relevant for possible deviations from the Gell-Mann–Okubo mass formula, R₁ and R₂ for the equal spacing rule of the decuplet. R₁ and R₂ are expected to be negative, as shown in Section 8.2. The effect is of the order of 5–10% in magnitude for typical choices m_s < ∼ m_q, as seen in Fig. 11.1, where various power-law potentials r^β and quark mass ratios m_s∕m_q are used. The ratios R₁ and R₂ were already displayed in Ref. [58] in a slightly different way. It is shown, in particular, that one hardly differentiates a three-body Y-shape potential (see Eq. 9.14) from a genuinely additive linear potential.

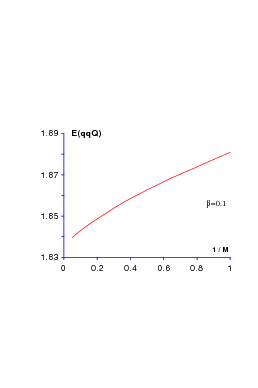
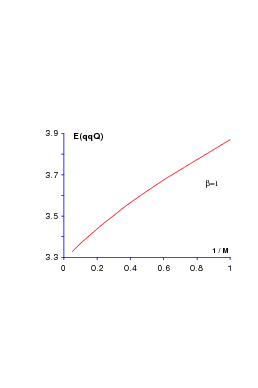
In Fig. 11.2, we show the variations of the binding energy of qqQ as a function of the inverse of the mass m_Q of the heavy quark. The energy qqQ is almost linear in m_Q⁻¹, as conjectured in Ref. [87].

Figure 11.1: Scale independent ratios R₁ = {2[qqq]+2[qqQ]−4[QQq]}∕{[qqq]−[QQQ]} and R₂ = {2[QQQ] + 2[QQq] − 4[qqQ]}∕{[qqq] − [QQQ]} for the power-law potentials ∑ r_ij^β with β = 0.1 and β = 1, as a function of the quark mass ratio x = M∕m.

Figure 11.2: Binding energy of qqQ, as a function of the inverse mass m_Q⁻¹ for the power–law potentials ∑ r_ij^β with β = 0.1 and β = 1.

[next] [front] [up]