Hyperfine splitting of heavy baryons

11.3 Hyperfine splitting of heavy baryons

We now come back to the Σ − Λ and Σ^∗− Σ splittings and examine how they behave if the mass of the strange quark is increased. In Fig. 11.5, we plot the value of

R = ΣQ--−-ΛQ--⋅ 7 Σ ∞ − Λ ∞

(11.12)

Figure 11.5: Ratios R₇ = (Σ_Q − Λ_Q )∕(Σ_∞ − Λ_∞ ) and R₈ = (Σ_Q^∗ − Σ_Q)∕(Σ_∞− Λ_∞) for the power-law potentials ∑ r_ij^β with β = 0.1 and β = 1, as a function of the quark mass ratio M∕m

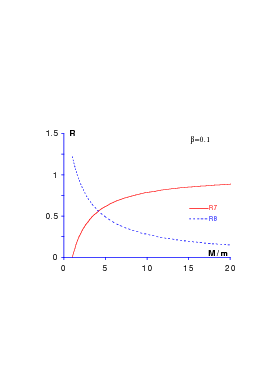
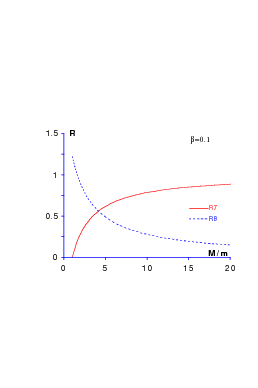
as a function of the ratio x = m_Q∕m_q. In the simple model (11.4), it is

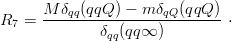M δ (qqQ ) − m δ (qqQ ) R7 = ---qq-----------qQ-------⋅ δqq(qq∞ )

(11.13)

The sharp variation is responsible for the observed increase from Σ − Λ = 77 MeV to Σ_c − Λ_c = 168 MeV. The Σ_b should also be unstable, thanks to its pionic decay to Λ_b. On the other hand, the ratio

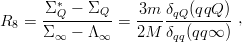Σ-∗Q-−-ΣQ-- 3m--δqQ-(qqQ-) R8 = Σ − Λ = 2M δ (qq∞ ) , ∞ ∞ qq

(11.14)

where the latter expression refers to model (11.4), goes to zero as the quark mass m_Q increases. Thus, the decay mode Σ_Q^∗ → Σ_Q + π becomes forbidden for heavy flavours and the experimental disentangling of Σ_Q and Σ_Q^∗ is difficult. The value of R₈ is shown in Fig. 11.5 for simple models.

The analysis is rather simple for doubly-flavoured baryons QQq . The light quark has a reduced mass close to m_q, so that its wave function is almost independent of m_Q. It experiences the potential of a localized diquark of spin 1. Hence, one expects

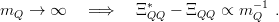m → ∞ =⇒ Ξ ∗ − Ξ ∝ m −1 . Q QQ QQ Q

(11.15)

Already, Fleck [73, 7], with a central potential V ∝ r^0.1 and a contact interaction (11.4), obtained

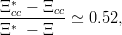Ξ ∗cc − Ξcc Ξ-∗-−-Ξ-- ≃ 0.52,

(11.16)

not too far from the quark mass ratio m_s∕m_c ≃ 0.32 which she used. The agreement would be much better for the comparison of Ξ_cc and Ξ_bb. More hyperfine splittings have been analysed recently by Anselmino et al.[105].

[next] [prev] [prev-tail] [front] [up]