11.5 The charge radius of the neutron

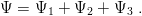
So far, the applications of the spin–spin potential (11.4) were restricted to mass splittings such as Δ–N. We now look at the effect of the hyperfine interactions on the wave function of the neutron. The spin–spin potential pushes the d quarks apart a little. In more technical terms, some mixed-symmetry components are introduced into the wave function.

The wave-function decomposition of Eq. (11.17) is now extended as

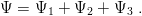(11.20)

The components Ψ₁ and Ψ₂ are associated with a symmetric spin–isospin wave function. The dominent component Ψ₁ is also symmetric in space variables, whereas Ψ₂ is of mixed symmetry and thus vanishes as δm = m_d − m_u goes to zero. The third component Ψ₃ is induced by the spin–spin interaction. It is symmetric, with both space and spin–isospin parts of mixed symmetry, as per eq. (3.33). It produces a small difference between the r.m.s. radii 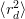and 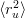and thus a non-vanishing charge radius squared

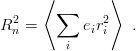(11.21)

If one neglects here isospin breaking, it is given by

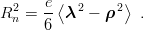(11.22)

At first approximation, Ψ₁ is dominated by its hyperscalar componenent π^−3∕2u ₀(ξ)∕ξ^5∕2, and Ψ ₃ by its lowest hyperspherical harmonics with grand orbital momentum L = 2,

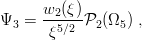(11.23)

where 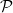₂(Ω₅) denotes the mixed-symmetry pair made out of 2π^−3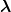∕2(2 −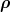2)∕ξ² and 4π^−3∕2(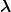 ⋅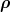)∕ξ², appropriately combined with the spin and isospin wave functions. This gives

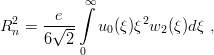(11.24)

and, when the spin–spin interaction (11.4) is treated at first order,

(11.25)

Once again, equations of this type are not equivalent to a mixing between closest neighbours of the unperturbed Hamiltonian.

With the model given in Eqs. (11.18) and (11.19), one obtains R_n² = −0.047 e.fm² and slightly larger values with sharper confinement. The experimental value [5], which is R_n² = −0.10 e.fm², probably receives contributions from other effects. For instance, in chiral bag models [14, 104], the neutron often consists of a proton-like core surrounded by a π⁻ cloud.