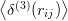 (more generally, the variations of
the wave function, when hyperfine effects are treated beyond first order);
(more generally, the variations of
the wave function, when hyperfine effects are treated beyond first order);
In the constituent-quark model, the isospin breaking of hadron masses results from several contributions, namely
i) the quark mass difference δm = md − mu;
ii) the induced change δE of the binding energy;
iii) the change in strength of the chromomagnetic interaction, that is proportional to (mimj)−1
and the variation of the correlation coefficient δij = 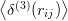 (more generally, the variations of
the wave function, when hyperfine effects are treated beyond first order);
(more generally, the variations of
the wave function, when hyperfine effects are treated beyond first order);
iv) the electromagnetic interactions between the charged quarks.
In several cases, these contributions tend to cancel each other out. This implies that they have to be computed carefully. Besides this technical aspect, this also means that the model dependence will be much amplified in the selected cases where the cancellation does not occur. For instance, Lane and Weinberg [106] have predicted much smaller splitting among Σc’s than did de Rújula et al.[103] who used a simpler ansatz to extrapolate matrix elements from ordinary to charmed hadrons.
When comparing the above contributions i) and ii), one is reminded that the non-relativistic approximation is never worse than for open flavours. Likewise, the electron is more relativistic in hydrogen than in positronium. If δE + δm < 0 when the u quark is replaced by d (contributions iii) and iv) being provisionally forgotten), we are in a paradoxal regime were the resulting hadron mass decreases as the mass of one of the constituents is increased. This is a warning that relativistic corrections are required [107].
To be specific, consider the neutron-to-proton mass difference. To zeroth order, n and p are degenerate, with a symmetric spatial wave function. If now the mass difference δm and electromagnetic interaction are switched on, small mixed-symmetry components are allowed, that can be treated perturbatively, exactly as the non-potential harmonics of Section 5.4 (the usual source of inaccuracy in this type of calculations consists of selecting a priori a few neighbouring states of the unperturbed Hamiltonian that are believed to mix with the main component; the Sternheimer equations of Section 5.4 are by far more powerful [50]). One can even optimize the starting point by adopting an inverse constituent mass m−1 = (2m u−1 + m d−1)∕3 for the proton and m−1 = (2m d−1 + m u−1)∕3 for the neutron, before implementing the corrections i)–iv).
In the hyperspherical formalism, the wave function is expanded as
 ∑ v[K ](ξ)
Ψ (ρ,λ ) = Ψ1 + Ψ2 = ---5∕2--Q [L](Ω5) + --5∕2-P [K ](Ω5 ) .
[L]∈S1 ξ [K ]∈S2 ξ](baryon1470x.png) | (11.17) |
The set S1 contains the symmetric HH and S2 those of mixed symmetry. The problem is first solved with S1 only, as in Chapter 5, and then the effect of S2 is studied by means of inhomogeneous equations similar to Eqs. (5.23) and (5.24).
Richard and Taxil [107] consider, among others, the following model:
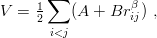 | (11.18) |
supplemented by the spin–spin term of Eq. (11.4), treated perturbatively. They obtained a good fit of ground-state baryons with the parameters (all units are appropriate powers of GeV)
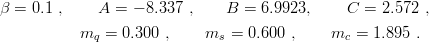 | (11.19) |
Then SU(2) is explicitly broken by using different constituent masses for u and d, mu = 0.300 and md = 0.313 GeV, with the results displayed in Table 11.1.
| β | δm | Central δE | Chromomag. | Electrostatic | Magnetic | Total |
| 0.1 | 13 | −8.5 | −2.7 | −0.7 | 0.2 | 1.3 |
| 1.0 | 2 | −0.2 | −0.4 | −0.3 | 0.002 | 1.2 |
Also shown are the values obtained with a linear potential model (β = 1), for which the fit of experimental splittings suggested a much smaller δm. These two models predict very similar mn − mp but differ widely in the charm sector. The situation for charmed baryons is analysed by Capstick [106] with references to earlier works.