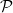 0 = π−3∕2. For each L, one
constructs the potential harmonic as being the linear combination which is maximally coupled to
0 = π−3∕2. For each L, one
constructs the potential harmonic as being the linear combination which is maximally coupled to
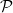 0. It is
0. It is
The coupled equations (5.8) can be solved by several numerical means. For instance, one can use the discretization algorithm described in Section 2.4 for mesons, which is easily generalized to coupled equations.
Although present computers allow one to diagonalize very large matrices, it seems desirable to optimize the efficiency of the method. The main question deals with the HH one has to actually include in the hyperspherical expansion (5.6). A simple strategy consists of taking all HH of appropriate quantum numbers up to a value Lmax of the grand orbital momentum and studying the convergence as Lmax increases. In fact, for a given L, only a few HH contribute significantly. This leads to the improved strategy of
potential harmonics [53]. Consider for instance the ground state, whose wave function is scalar
and symmetric. Then the lowest and dominant harmonics is 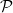 0 = π−3∕2. For each L, one
constructs the potential harmonic as being the linear combination which is maximally coupled to
0 = π−3∕2. For each L, one
constructs the potential harmonic as being the linear combination which is maximally coupled to
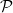 0. It is
0. It is
![∑ V P
RL = (----0,[L])[L]-,
∑ V 2 1∕2
0,[L]](baryon1206x.png) | (5.20) |
where the summation runs over the magnetic numbers associated with L. It is coupled to 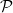 0
through the transition potential
0
through the transition potential
![(∑ 2 )1∕2
⟨0 |V | RL ⟩ = V0,[L]](baryon1207x.png) | (5.21) |
The word
potential comes from 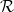 L containing the harmonics that are present in the expansion of the
potential itself. For power-law potentials,
L containing the harmonics that are present in the expansion of the
potential itself. For power-law potentials,  L is independent of ξ. For general potentials,
L is independent of ξ. For general potentials,  L
depends on ξ, but the method remains applicable [53].
L
depends on ξ, but the method remains applicable [53].
In practice, one can first compute the bound state in the approximation of potential harmonics,
with a fairly large Lmax. Then the effect of non-potential harmonics of low L, say 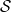 [L], can be
estimated by solving Sternheimer-type equations. If
[L], can be
estimated by solving Sternheimer-type equations. If
![∑ ∑ w (ξ)
Ψ (ρ, λ) = vL(ξ)RL (Ω5 ) + -[L]--S [L](Ω5) ,
L ξ5∕2 [L] ξ5∕2](baryon1208x.png) | (5.22) |
at first order
![1- ′′ (L-+-3∕2)(L-+-5∕2-) [ ]
m w [L](ξ) − m ξ2 w[L](ξ) + E0 − V [L],[L ](ξ) w [L](ξ)
∑ ∑ ,
= V [L],L′(ξ)vL′(ξ) + V[L],[L ]′(ξ )w [L ]′(ξ )
L′ [L ]⁄=[L]′](baryon1209x.png) | (5.23) |
where E0 is frozen to its value at the approximation of potential harmonics. The second-order correction to the energy is
V[L],L′(ξ)uL′(ξ)dξ .
L ′,[L] 0](baryon1210x.png) | (5.24) |
In practice, one often neglects the last term in Eq. (5.22), which only contributes to higher orders: then the corrections can be computed separately for each non-potential harmonic.