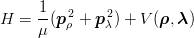
Let us consider now a baryon made of different quarks. We use the Jacobi coordinates of Eq. (3.52) and the corresponding reduced mass μ = 2m1m2∕(m1 + m2). If two quarks are identical, as in Λ, Σ or Ξ type of baryons, or almost identical, as s and u in Ξc+, they are assigned to labels 1 or 2. This helps to enforce the exact or approximate symmetry constraints. The hyperspherical treatment of
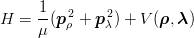 | (5.25) |
is then performed as for identical quarks. There are, however, more harmonics into the expansion, since some (if m1 = m2≠m3) or all (if m1≠m2≠m3) symmetry constrains are relaxed. This makes the use of potential harmonics more desirable.
In Ref. [58] is studied the case of harmonic forces, for which an exact solution is available. The results of the linear model V = 1 2 ∑ rijβ with β = 1, m 1 = m2 = 1, and m3 = m′ are shown in Table 5.3. Another example, more suited to double-charm baryons [7] is given in Table 5.3. The hyperscalar approximation is obviously rather poor for the wave function. However, the convergence remains satisfactory as Lmax increases.
| β | m′ | Lmax | E0 | δ(3)(r 12) | δ(3)(r 13) |
| 0 | 3.4671 | 0.0468 | 0.1006 | ||
| 2 | 3.4405 | 0.0569 | 0.0924 | ||
| 1 | 5 | 4 | 3.4381 | 0.0587 | 0.0944 |
| 6 | 3.4380 | 0.0595 | 0.0945 | ||
| 8 | 3.4379 | 0.0598 | 0.0949 | ||
| 0 | 5.0372 | 0.0819 | 0.0158 | ||
| 2 | 4.9523 | 0.0503 | 0.0193 | ||
| 1 | 0.2 | 4 | 4.9303 | 0.0530 | 0.0203 |
| 6 | 4.9393 | 0.0522 | 0.0205 | ||
| 8 | 4.9392 | 0.0523 | 0.0206 | ||
| 0 | 1.9481 | 1.1891 | 0.2289 | ||
| 2 | 1.9463 | 0.8866 | 0.2706 | ||
| 0.1 | 0.2 | 4 | 1.9453 | 0.9972 | 0.2932 |
| 6 | 1.9452 | 0.9853 | 0.2980 | ||
| 8 | 1.9452 | 0.9983 | 0.3018 | ||