[next] [tail] [up]

5.1 Basic formalism

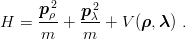
Let us start with the equal mass case, i.e., the reduced Hamiltonian

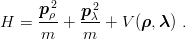p 2ρ p 2 H = ---+ -λ-+ V (ρ, λ) . m m
(5.1)

The two-body character of V is not crucial, but it greatly simplifies some of the computations, as we shall see. The 6-dimensional vector 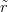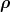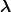˜r = (ρ,λ) is written in spherical coordinates

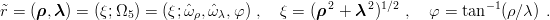˜r = (ρ,λ ) = (ξ;Ω5) = (ξ; ˆω ρ,ωˆλ,φ) , ξ = (ρ 2 + λ 2)1∕2 , φ = tan− 1(ρ∕ λ) .
(5.2)

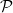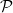We now introduce a complete set of 6-dimensional spherical harmonics P[L](Ω5), where [L] denotes the grand orbital momentum L = 0, 1, 2… and its associated magnetic numbers, i.e., the generalization of the familiar spherical harmonics Y lm. One may define L more precisely by saying that ξLP [L](Ω5) is a harmonic polynomial of degree L in 6 dimensions [56],

( ) ( ) Δ6 ξLP [L](Ω5 ) ≡ (Δρ + Δ λ) ξLP [L](Ω5 ) = 0 .
(5.3)

In spherical coordinates, this leads to the equation

[ ] 2 2 2 -∂2- ∂-- L P [L ](Ω5) = lρ + lλ − ∂ φ2 − 4 cot2φ ∂φ P [L](Ω5) = L (L + 4)P [L](Ω5)
(5.4)

associated with the normalization condition

∫ P[∗L](Ω5 )P[L]′(Ω5)dΩ5 = δ[L],[L]′ ,
(5.5)

One expands the baryon wave function into hyperspherical harmonics (HH)

∑ Ψ(ρ, λ) = u[L](ξ)P (Ω ) , ξ5∕2 [L] 5 [L]
(5.6)

so that the Schrödinger equation HΨ = EΨ, whose expression in spherical coordinates reads

[ ] --1----d2- 5∕2 -1 L2-+-15∕4- m ξ5∕2dξ2 ξ − m ξ2 + E − V (ξ,Ω5) Ψ = 0 ,
(5.7)

becomes equivalent to the infinite set of coupled radial equations

1 (L + 3∕2)(L + 5 ∕2) [ ] -- u′′[L](ξ) − ----------2--------u[L](ξ) + E − V [L],[L](ξ) u [L](ξ) m m ξ ∑ , = V[L],[L]′(ξ)u[L]′(ξ) [L]⁄=[L]′
(5.8)

∫ ∗ V [L],[L]′(ξ) = dΩ5P [L](Ω5 )V (ξ,Ω5)P [L]′(Ω5 ) .
(5.9)

Clearly, solving the three-body problem that way implies overcoming the following difficulties: listing the appropriate HH, computing the angular projections (5.9) and solving the above coupled equations.

[next] [front] [up]