5.3 The radial potentials

The potentials which enter into the coupled equations are given by Eq. (5.9). For simple two-body potentials inserted between the scalar harmonics of Simonov, the corresponding integral can be carried out analytically [53, 54]. Otherwise, the computation is more painful. A possible strategy consists of expanding the potential itself into HH, say

(5.17)

where the summation is restricted to HH that are scalar and fully symmetric, i.e., of the type 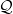_[L] = 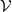_L^3ν′. Then

(5.18)

The so-called

3H coefficients which enter into the above expression are independent of the potential and thus can be stored once aand for all. They are given by

(5.19)

and are submitted to the selection rule |L − L′|≤ L′′≤ L + L′.