5.2 The hyperspherical harmonics
While there is only one HH with L = 0, namely 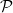 0 = π−3∕2, as L increases, the number of HH
grows quite fast. There are N(L) = (L + 1)5∕5! independent homogeneous polynomials of degree L
with 6 variables, and N(L) −N(L− 2) independent linear combinations of these are harmonic. So,
if one operates without care, one would end up with a very large number of HH, even if the cut-off
Lmax in the expansion (5.6) is small.
0 = π−3∕2, as L increases, the number of HH
grows quite fast. There are N(L) = (L + 1)5∕5! independent homogeneous polynomials of degree L
with 6 variables, and N(L) −N(L− 2) independent linear combinations of these are harmonic. So,
if one operates without care, one would end up with a very large number of HH, even if the cut-off
Lmax in the expansion (5.6) is small.
A complete set of HH is provided by the following functions which are eigenstates of the
individual orbital momenta lρ and lλ:
![P = N (sin φ)lρ(cos φ)lλPlρ+1∕2,lλ+1∕2Y mρ(ω )Y mλ (ω ) ,
[L] n lρ ρ lλ λ](baryon1187x.png) | (5.10) |
where one has introduced the Jacobi polynomials Pnα,β [28] and the normalization
coefficient
![{ 2(2n + lρ + l + 2)n!(n + lρ + l + 1)!}1∕2
N = ------------λ-----------------λ------ ⋅
π [2(n + lρ) + 1]!![2(n + lλ ) + 1]!!](baryon1188x.png) | (5.11) |
The integer n, which corresponds to the degree of the Jacobi polynomial, is submitted to the
constraint
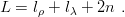 | (5.12) |
Harmonics of given total (ordinary) angular momentum 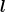 =
= 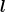 ρ +
ρ + 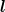 λ (not to be confused with the
grand orbital momentum L) are constructed by Clebsch–Gordan coupling of the HH (5.10). One
should further restrict the expansion (5.6) to these HH having the desired permutation
properties.
λ (not to be confused with the
grand orbital momentum L) are constructed by Clebsch–Gordan coupling of the HH (5.10). One
should further restrict the expansion (5.6) to these HH having the desired permutation
properties.
There are several ways of constructing HH of given angular momentum, parity and
permutation symmetry. One method consists of using harmonic-oscillator wave functions
and removing the Gaussian factor exp(−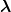 2 −
2 −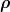 2). More details will be provided in
Section 8.2 where we come back to the link between the harmonic oscillator and the HH
expansion.
2). More details will be provided in
Section 8.2 where we come back to the link between the harmonic oscillator and the HH
expansion.
A direct construction of symmetrized HH has been given by Simonov [40], who made great use
of the complex vectors λ + iρ and λ−iρ to solve the Laplace equation (5.3). For the case of scalar
harmonics (lP = 0+), he arrived at the compact expressions
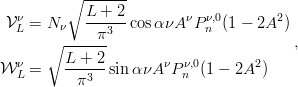 | (5.13) |
where the scalar variables A and α are introduced
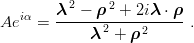 | (5.14) |
The integer ν runs from L∕2 to 0, in steps of 2, so that the degree of the Jacobi polynomial,
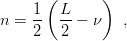 | (5.15) |
remains acceptable, i.e., n ≥ 0. The normalization factor is Nν = 1 if ν≠0 and Nν = 2−1∕2 if ν = 0.
All permutation properties of the above harmonics are contained in the cos αν or sin αν factors: if
ν = 3ν′ (ν′ integer) then 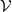 Lν is symmetric and
Lν is symmetric and 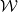 Lν, if non-vanishing, antisymmetric; otherwise,
Lν, if non-vanishing, antisymmetric; otherwise,
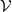 Lν and
Lν and 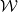 Lν form a pair of mixed symmetry.
Lν form a pair of mixed symmetry.
In principle, one can write down the HH of any given angular momentum l and projection
lz = M, parity P and permutation properties. Barma and Mandelzweig [54], using earlier
work [57] on the permutation group, propose
![∑ l
P [L] ∝ exp iα ν DlMm (α1, α2,α3)Fm (A ) ,
m=− l](baryon1198x.png) | (5.16) |
where α1,α2 and α3 are the Euler angles defining the position of the particle plane (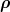 ,
,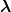 ) with
respect to fixed axes and are thus expressable in terms of
) with
respect to fixed axes and are thus expressable in terms of 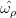 and
and 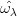 ; DMml are the Wigner
rotation functions; Fm(A) are given by a differential equation that is deduced from the original
equation (5.3) or (5.4). However, no concise expression as simple as (5.13) can be exhibited for
general l.
; DMml are the Wigner
rotation functions; Fm(A) are given by a differential equation that is deduced from the original
equation (5.3) or (5.4). However, no concise expression as simple as (5.13) can be exhibited for
general l.
 0 = π−3∕2, as L increases, the number of HH
grows quite fast. There are N(L) = (L + 1)5∕5! independent homogeneous polynomials of degree L
with 6 variables, and N(L) −N(L− 2) independent linear combinations of these are harmonic. So,
if one operates without care, one would end up with a very large number of HH, even if the cut-off
Lmax in the expansion (5.6) is small.
0 = π−3∕2, as L increases, the number of HH
grows quite fast. There are N(L) = (L + 1)5∕5! independent homogeneous polynomials of degree L
with 6 variables, and N(L) −N(L− 2) independent linear combinations of these are harmonic. So,
if one operates without care, one would end up with a very large number of HH, even if the cut-off
Lmax in the expansion (5.6) is small.
![P = N (sin φ)lρ(cos φ)lλPlρ+1∕2,lλ+1∕2Y mρ(ω )Y mλ (ω ) ,
[L] n lρ ρ lλ λ](baryon1187x.png)
![{ 2(2n + lρ + l + 2)n!(n + lρ + l + 1)!}1∕2
N = ------------λ-----------------λ------ ⋅
π [2(n + lρ) + 1]!![2(n + lλ ) + 1]!!](baryon1188x.png)
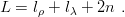
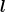 =
= 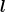
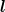
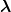
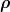
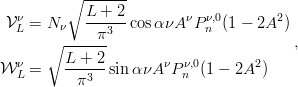
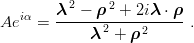
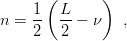
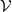
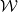
![∑ l
P [L] ∝ exp iα ν DlMm (α1, α2,α3)Fm (A ) ,
m=− l](baryon1198x.png)
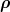
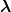 ) with
respect to fixed axes and are thus expressable in terms of
) with
respect to fixed axes and are thus expressable in terms of 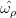 and
and 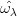 ;
;