8.3 Lowest excitation

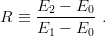
So far, we have studied separately the ordering and splitting of positive-parity excitations and the corresponding pattern of the negative-parity states. We now address the following question: which is the lowest excitation? the positive-parity radial excitation ∣1⟩≡ [56, 0⁺]′ or the negative-parity orbital excitation ∣2⟩≡ [70, 1⁻]? This question is motivated by the anomalously low location of the Roper resonance in the excitation spectrum of N and Δ. In the case of harmonic confinement, the radial excitation energy E₁ is twice as high as the orbital excitation E₂, say R = 1∕2, where

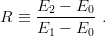(8.34)

For a hyperscalar Coulombic potential V = −(r₁₂² + r ₂₃² + r ₃₁²)^−1∕2, one gets the degeneracy R = 1.

For a general potential V (1,2,3), invariant under rotations and translations, and symmetric, but not necessarily pairwise, one remarks that the same projection governs the radial equations of ∣1⟩ and ∣2⟩. As seen in Eqs. (8.30) and (8.31), this is V ₀(ξ), the hyperscalar projection of the potential. At this approximation (hereafter denoted E_i^hs), one has to compare the eigenvalue equations (i = 1, 2),

(8.35)

n_i being the usual radial (Liouville) index. One can now use the Coulomb theorem (2.36), which is immediately applicable to half-integer values of l and one obtains

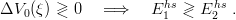(8.36)

One can elaborate a little on the above condition, in the simple case of a two-body interaction, for which [53]

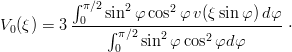(8.37)

Obviously, if v(r) is concave (convex) in r⁻¹, V ₀(ξ) will be concave (convex) in ξ⁻¹ and the theorem (8.36) will be applicable. Thus, with any plausible interquark potential, we obtain

(8.38)

at the lowest order in the hyperspherical expansion [82]. The effect is rather pronounced, since R ≃ 0.7 for a linear potential. For such smooth and symmetric potentials, the corrections E_i −E_i^hs due to higher hyperspherical harmonics are extremely small and cannot change the level order. This is confirmed by numerical calculations.

More challenging is the case of a gravitational interaction

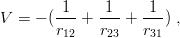(8.39)

which, at first approximation, gives rise to the hyperscalar potential proportional to −(r₁₂² + r ₂₃² + r ₃₁²)^−1∕2. At this approximation, E ₁ = E₂. The breaking of the E₁ = E₂ degeneracy has been studied numerically by S. Fleck [73], whose work updates that of Ref. [82]. She computed the successive approximations 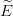₁(L_max) and 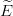₂(L_max) as a function of the maximal

grand orbital momentum L_max introduced in the wave function. It appears clearly that E₂ > E₁ when one approaches convergence.