6.4 Results
We present below some results concerning the symmetric J = 0 case, i.e., the [56, 0+] states in our
previous notation. We first notice that, for the harmonic oscillator, the partial-wave expansion is
exactly restricted to angular momenta a = b = 0. It is thus useful to test the algorithms by solving
Eq. (6.8) with V (ρ) = ρ2.
Let us now consider the linear potential V (r) = 1
2 ∑
rij and analyse the results as a function of
the maximal orbital momentum amax introduced in the partial-wave expansion (6.7). A well-known
trick consists of shifting the potential, to optimize the dominance of the a = 0 partial wave and
ensure a nice asymptotic decrease of the Faddeev component Ψ3 [66]. More precisely,
one performs the computation with V = ∑
[1
2rij − v0] and eventually adds 3v0 to the
eigenvalues. The results shown in Table 6.1 have been obtained with v0 = 2. Preliminary
investigations have confirmed that the results look much better for such large values of
v0.
The accuracy is not impressive for the eigenenergies, at least when they are computed as
eigenvalues of the coupled integro-differential equations (6.8). This could probably be improved by
recomputing the energy as 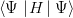 [66]. On the other hand, one should stress the impressive
quality of the Faddeev wave function. With only the lowest partial wave a = b = 0,
the correlation coefficient δ12 is obtained almost exactly. We have seen in the previous
chapters that it was very painful to achieve a decent convergence for δ12 with variational
methods.
[66]. On the other hand, one should stress the impressive
quality of the Faddeev wave function. With only the lowest partial wave a = b = 0,
the correlation coefficient δ12 is obtained almost exactly. We have seen in the previous
chapters that it was very painful to achieve a decent convergence for δ12 with variational
methods.
Table 6.1: Binding energy and short-range correlation coefficient of the two first JP = 0+
levels in the linear potential V = 1
2 ∑
rij, with quark masses mi = 1, obtained by solving
the Faddeev equations. The substraction constant is v0 = 2 and amax denotes the maximal
orbital momentum in the Faddeev amplitude.
|
|
|
|
|
| amax | E0,0 | δ12n=0 | E
1,0 | δ12n=1 |
|
|
|
|
|
| 0 | 3.863 | 0.0566 | 5.318 | 0.0565 |
| 2 | 3.862 | 0.0570 | 5.317 | 0.0568 |
|
|
|
|
|
| |
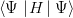 [66]. On the other hand, one should stress the impressive
quality of the Faddeev wave function. With only the lowest partial wave a = b = 0,
the correlation coefficient δ12 is obtained almost exactly. We have seen in the previous
chapters that it was very painful to achieve a decent convergence for δ12 with variational
methods.
[66]. On the other hand, one should stress the impressive
quality of the Faddeev wave function. With only the lowest partial wave a = b = 0,
the correlation coefficient δ12 is obtained almost exactly. We have seen in the previous
chapters that it was very painful to achieve a decent convergence for δ12 with variational
methods.