6.1 Basic equations

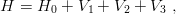
We follow here the approach of Noyes [62], Merkuriev [63] and the Grenoble group [64]. Let us consider the symmetric Hamiltonian

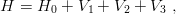(6.1)

where H₀ is the relative kinetic energy of the three identical quarks (thus free of centre-of-mass motion), and V ₁ = V (r₂₃) and so on. We use the Jacobi variables of Eq. (3.18) = ⁽³⁾ and 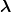= 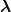⁽³⁾ as well as the other variables 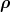⁽ⁱ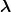⁾, ⁽ⁱ⁾ deduced by the circular permutation (3.30).

Let us search for a symmetric eigenstate Ψ(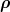,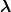), which could be, for instance, the ground state with spin S = 3∕2, in the form

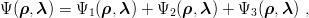(6.2)

where

i) Ψ₃ is even in ;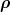

ii) Ψ₃ has the same short-range and long-range behaviour as the total wave function Ψ(,);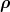

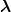iii) the other components Ψ_i are deduced by circular permutation, namely

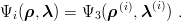(6.3)

Clearly, the set of equations

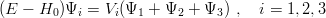(6.4)

implies the desired Schrödinger equation HΨ = EΨ for the total wave function Ψ. The uniqueness of the Faddeev decomposition does not raise much problem in this bound-state problem, unlike in scattering situations with three or more particles, for which this delicate question is discussed, e.g., by Merkuriev [63] or Omnes [65].

For identical particles, one has simply tosolve the equation

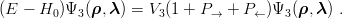(6.5)

For an antisymmetric state, one constrains Ψ₃ to be odd in 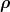. For a state of mixed symmetry, the parenthesis is replaced by (1 + jP_→ + j²P _←).