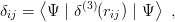
In a variational calculation, it is much more difficult to reproduce short-range behaviour of the wave function than the binding energy. Let us compare the zero-range correlations
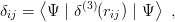 | (4.22) |
which is used in the perturbative treatment of hyperfine splittings (see Chapter 8). We consider again V = 1 2 ∑ rij and i) qqq (mi = 1), ii) qqQ (mi = 1, 1, 5), and iii) QQq (mi = 1, 1, 0.2), in Table 4.6. We remark that when we try to optimize the oscillator parameter in the h.o. expansion (large N′) too much, we do not gain significantly on the binding energy (see Table 4.1), but we get very poor results for short-range correlations. On the other hand, one obtains decent values by fixing the parameter at the lowest approximation (N′ = 0) and then pushing the expansion further. These are rather general properties of variational calculations [50]. The optimization of the energy forces the approximate wave function to match the exact one at intermediate distances. If the asymptotic behaviour is poorly reproduced, one has to compensate at short distances to preserve the normalization.
| Case |
| δ12 | δ13 | Gaussian | δ12 | δ13 | |||
| N = 0 (N′ = 0) | 0.0507 | 0.0507 | 1S | 0.0507 | 0.0507 | ||||
| N = 2 (N′ = 0) | 0.0507 | 0.0507 | 2S | 0.0547 | 0.0547 | ||||
| qqq | N = 4 (N′ = 4) | 0.0471 | 0.0471 | 3S | 0.0550 | 0.0550 | |||
| N = 6 (N′ = 4) | 0.0473 | 0.0473 | 1S+1D | 0.0516 | 0.0516 | ||||
| N = 8 (N′ = 4) | 0.0478 | 0.0478 | 2S+1D | 0.0556 | 0.0556 | ||||
| N = 0 (N′ = 0) | 0.0430 | 0.0926 | 1S | 0.0534 | 0.0843 | ||||
| N = 2 (N′ = 0) | 0.0517 | 0.0851 | 2S | 0.0582 | 0.0906 | ||||
| qqQ | N = 4 (N′ = 4) | 0.0507 | 0.0829 | 3S | 0.0595 | 0.0905 | |||
| N = 6 (N′ = 4) | 0.0519 | 0.0830 | 1S+1D | 0.0533 | 0.0870 | ||||
| N = 8 (N′ = 4) | 0.0526 | 0.0839 | 2S+1D | 0.0581 | 0.0932 | ||||
| N = 0 (N′ = 0) | 0.0754 | 0.0145 | 1S | 0.0462 | 0.0184 | ||||
| N = 2 (N′ = 0) | 0.0469 | 0.0176 | 2S | 0.0487 | 0.0201 | ||||
| QQq | N = 4 (N′ = 4) | 0.0505 | 0.0183 | 3S | 0.0515 | 0.0201 | |||
| N = 6 (N′ = 4) | 0.0484 | 0.0188 | 1S+1D | 0.0461 | 0.0186 | ||||
| N = 8 (N′ = 4) | 0.0494 | 0.0191 | 2S+1D | 0.0486 | 0.0203 | ||||