Empirical variational methods

4.5 Empirical variational methods

As already acknowledged, the h.o. expansion (as well as the hyperspherical expansion of Chapter 5) suffers from being a little heavy, especially in the case of unequal masses. Its main advantage is that convergence can eventually be reached, provided one pushes the calculation far enough. Now, there exist many alternative parametrizations of the trial wave function which immediately provide a dramatic accuracy, though they are a little empirical in nature. We shall present below the example of the parametrization of the wave function in terms of Gaussian functions. This method is copiously used in theoretical molecular physics.

Let us introduce the method in the simple two-body case. The radial wave function is written

[ ] 1 un,l(r) ∑q Γ (32 ) 2 √ --- l( αi) 34 1 2 Rn,l = --r----= ci ---3---- ( αir) π-- exp − 2αir , i=1 Γ (2 + l)

(4.17)

and the α_i’s and the c_i’s are optimized, the latter being subject to a normalization constraint. For given α_i’s, the c_i’s are obtained by a simple matrix diagonalization. The α_i’s are determined by standard minimization algorithms. The choice of the above parametrization leads to easy calculation of the matrix elements, most often in terms of elementary functions. With only the q = 1 term, the method coincides with the N = 0 order of the h.o. expansion. The comparison for increasing q and N is shown in Table 4.4, for angular momentum l = 0, reduced mass μ = 1, and potential V (r) = r. The Gaussian expansion is clearly more efficient here.

Table 4.4: Comparison of the harmonic oscillator expansion and Gaussian expansion for the two-body linear potential. The exact values given by the first zero of the Airy function is 2.33811...

Number

of terms

Harmonic oscillator

Gaussian

N = 0 2.34478

q = 1 2.34478

N = 2 2.34478⁽¹⁾

q = 2 2.33825

N = 4 2.33841

q = 3 2.33811

⁽¹⁾The Moshinsky theorem [49] strikes again.

Consider now the case of symmetric baryons (qqq). The starting point coincides with the N = 0 order of the h.o. expansion

S ( α)3 ∕2 [ 1 2 2 ] Ψ = φα = π exp − 2α (ρ + λ ) .

(4.18)

We name it

1S for

1 Gaussian with l_ρ = l_λ = 0. We similarly define

2S,

3S,…parametrizations by superposing q = 2, 3…of these Gaussians.

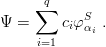∑q Ψ = ciφSαi . i=1

(4.19)

Incursions into the l_ρ = l_λ > 0 sectors provide configurations

qP,

qD which can be added to the

qS ones. This makes use of

P -2-- S φ α(ρ, λ) = √3-α ρ ⋅ λ φα (ρ, λ) [ ] φDα(ρ, λ) = -√2--α2 3(ρ ⋅ λ )2 − ρ2λ2 φSα (ρ,λ), etc. 3 5

(4.20)

For the qqq ground state with quarks of mass m = 1 bound by V = 1 2 ∑ r_ij, one obtains the results of Table 4.5.This is comparable to a harmonic-oscillator expansion pushed up to N = 6.

Consider now the cases of qqQ and QQq baryons, with constituent masses (1, 1, 5) and (1, 1, 0.2), respectively, and the same V = 1 2 ∑ r_ij. The terms of the variational wave function can now have different Gaussian parameters for the ρ and λ parts. For instance

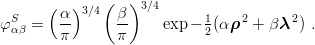( ) S (α-)3∕4 β- 3∕4 1 2 2 φ αβ = π π exp − 2(αρ + βλ ) .

(4.21)

The results are shown in Table 4.5. With only one term, one already obtains a good approximation because the trial wave function can adjust itself to the asymmetry of the system. Note that, for QQq, internal orbital excitations play a less important role than the detailed description of the S-wave sector.

Table 4.5: Empirical variational calculation of the binding energy of the ground state of the potential V = 1 2 ∑ r_ij for the quark masses m_i = 1 (qqq), m_i = 1, 1, 5 (qqQ), and m_i = 1, 1, 0.2 (QQq). The exact values are 3.8631, 3.4379, and 4.9392.


Parametrization	qqq	qqQ	QQq

1S	3.8711	3.4451	4.9498
2S	3.8648	3.4394	4.9414
3S	3.8647	3.4391	4.9400
1S+1D	3.8698	3.4441	4.9422
2S+1D	3.8634	3.4383	4.9408

[next] [prev] [prev-tail] [front] [up]