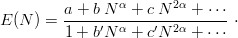
So far, we have presented variational calculations with straightforward optimization by explicitly varying the parameters and increasing the basis. One may now try to elaborate a little on the convergence pattern. For instance, one may study the variational energy E(N) as a function of the maximum number of states introduced into the h.o. expansion, and try to guess what E(∞) should be. To this end, E(N) can be written as a rational function
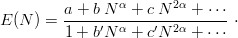 | (4.23) |
The trouble is, however, that the Padé coefficients a,b,… are determined with numerical errors, so one should not amplify the noise in the extrapolation.
We now turn to really
professional variational calculations [46]. They are generally based on Monte Carlo methods for determining the variation parameters and for computing the integrals that are needed. Papanicolaou and Spathis [51], for instance, expand the wave function on generalized coherent states and diagonalize the Hamiltonian on this basis. Some of their results are shown in Table 4.7. They correspond to quark masses mi = 1 and confining potential V = 1 2 ∑ rij0.1. They can be compared very favourably with the results shown in Table 5.1, obtained from the hyperspherical expansion applied to the same potential.
| State | E0 | 103δ 12 | |
| [56, 0+] | 1.88017 | 1.25 | |
| [70, 1−] | 1.9362 | ||
| [56, 0+]′ | 1.96231 | 0.93 | |
| [70, 0+] | 1.97256 | 0.98 | |
| [20, 1+] | 1.9885 | ||
| [70, 1−]′ | 1.9964 | ||
| [56, 1−] | 1.9982 | ||
| [70, 1−]′′ | 2.0145 | ||