General properties of variational solutions

4.2 General properties of variational solutions

It is amazing that variational solutions obey the same general theorems as the exact solutions. This was first pointed out in a remarkable article by Fock [48]. Let us give a few examples. We shall assume that the set of trial wave functions is globally invariant under rescaling i → λi.

i) Scaling laws. The variational approximation to a power-law interaction ∑ B_ijr_ij^β behaves like

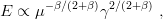E ∝ μ −β∕(2+β)γ2∕(2+ β) ,

(4.4)

if all quark masses are simultaneously multiplied by μ and strength coefficients B_ij by γ.

ii) Virial theorem. If Ψ is a variational approximation to H = T + V , T being the kinetic energy operator, then

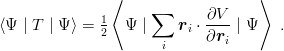⟨ ∑ ⟩ ⟨Ψ | T | Ψ ⟩ = 1 Ψ | ri ⋅ ∂V-| Ψ . 2 i ∂ri

(4.5)

iii) Convexity. Consider mesons for simplicity, bound by a flavour-independent potential. Then

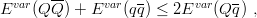Evar(QQ--) + Evar (qq) ≤ 2Evar(Qq ) ,

(4.6)

as for the true energies (see Section 2.7).

iv) Inequalities between mesons and baryons. If the trial wave function of baryons Ψ(1,2,3) belongs to the set of trial wave functions of mesons for any given 3, then

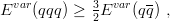var 3 var - E (qqq) ≥ 2E (qq) ,

(4.7)

provided one adopts the 1_ 2

rule V _qq = 1 2V _qq, which will be discussed in more detail in Chapter 9.

[next] [prev] [prev-tail] [front] [up]