7.1 The diquark–quark approximation

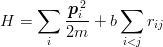
Diquarks are almost as old as quarks. The possibility that quarks might cluster pairwise in baryons, leading to a simple two-body structure, has been suggested by many authors since the early days of the quark model. There are currently many speculations on the use of diquarks to analyse baryon production in e⁺e⁻ experiments, in hadronization of jets, or in the decay of heavy particles [11]. We shall restrict ourselves here to the domain of baryon spectroscopy.

The first consequence of the extreme version of the quark–diquark picture would be a dramatic simplification of the spectrum. States like the [20, 1⁺] level of the N = 2 band of the harmonic oscillator, where both

ρ and

λ degrees of freedom are excited, should be absent in the diquark model. These states are, however, hardly formed in the usual meson–nucleon or photon–nucleon entrance channels, where spectator diagrams are favoured. Therefore, the distinction between the conventional three-quark model and the diquark–quark model requires high-statistics production experiments. This could be one of the goals of a future high-intensity hadron factory [67]. Another striking consequence of the extreme quark–diquark model would be the appearence of new types of hadrons. If diquarks are taken seriously as elementary constituents, then, besides ordinary hadrons which are mesons (quark–antiquark) and baryons (quark–diquark), one should find “diquonia” (diquark–antidiquark) and, perhaps, “dibaryons”. It is sufficient to say here that there is no firm experimental evidence for such states.

In a weaker version of the diquark model, one simply assumes that a diquark clustering occurs in baryons, leading to a simplified phenomenological picture in terms of a quark surrounding a diquark. This was, for instance, the point of view adopted by Lichtenberg et al.[68], who described ordinary mesons and baryons with a unique potential, the diquark mass being an adjustable parameter.

This suggests analysing rigorously to what extent diquark clustering actually results from the quark dynamics. For instance, it was claimed for many years that orbitally-excited baryons should consist of a quark and a diquark at both ends of a rotating string, with a colour (3 −3) structure, since the experimental Regge slope α′ (defined as M² = α′J) is the same as for mesons. Martin [11, 69] has shown that this clustering, in fact, results from the ordinary three-quark dynamics. He considered the Hamiltonian

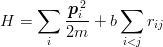(7.1)

and looked for the lowest classical configuration of given angular momentum l. For low l, the minimum corresponds to the symmetric configuration of an equilateral triangle. As l becomes larger, the minimum is obtained (modulo permutations) for r₁₂ = 0 and r₃₁ = r₃₂ = r. Since the quantum states of high l are sharply localized in a pocket of attraction between an external and an internal centrifugal barrier, the classical configuration is likely to provide a very good approximation of the quantum states. Martin [69] also analysed the case of a collective potential [70]

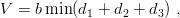(7.2)

where the sum of the distances linking the quarks to a junction is minimized with respect to the location of the junction. This corresponds to a generalization of the linear potential for mesons, where the chromoelectric flux has the minimal length from the quark to the antiquark. Relativistic kinematics was also considered in Ref. [69]. In each case, the same conclusion was reached: high l baryons seem to be of the quark–diquark type, in the semi-classical approximation.

A full quantum, but numerical, study was carried out in Ref. [71], with restriction to the non-relativistic case with pairwise interaction. Various flavour configurations of different angular momentum l were analysed. A first means of investigation consists of comparing the (q₁q₂q₃) three-body mass spectrum to the [(q₁q₂) −q₃] approximation, where one first computes the mass of the (q₁q₂) diquark out of the quark–quark potential v(r₁₂) and then the mass of the baryon as a diquark–quark state bound by the two-body potential V = 2v(r₃₁=r₃₂=r). This comparison of masses is a little disappointing. The agreement between the approximate and the exact masses is often accidental and does not imply a genuine diquark clustering inside the baryon.

Some three-body wave functions were also analysed in Ref. [71], for various flavour combinations and various angular momenta. In general, there is no diquark clustering in the wave function, with some noticeable exceptions:

– Ground-state baryons with two heavy quarks, QQq, look like a localized colour source QQ surrounded by a light quark q. The effect is, however, less and less pronounced for excited states, suggesting instead the use of the Born–Oppenheimer approximation, as discussed in the next section.

– At high angular momenta, baryons exhibit a clear quark–diquark structure (of course, in the case of identical quarks, several pair-clusterings are present to comply with the desired permutation symmetry, but they do interfere with each other). Again, this clustering results from the dynamics and does not require the help of mysterious short-range forces to keep the quarks together. For double-charm baryons, the asymptotic clustering is of the (Qq)–Q type, i.e., differs from the structure experienced by the ground state.